Linear complementarity problem
In mathematical optimization theory, the linear complementarity problem (LCP) arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case. It was proposed by Cottle and Dantzig in 1968.[1][2][3]
Contents |
Formulation
Given a real matrix M and vector q, the linear complementarity problem seeks vectors z and w which satisfy the following constraints:
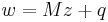
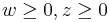 (that is, each component of these two vectors is non-negative)
(that is, each component of these two vectors is non-negative)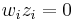 for all i. (The complementarity condition)
for all i. (The complementarity condition)
A sufficient condition for existence and uniqueness of a solution to this problem is that M be symmetric positive-definite.
The vector 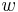 is a slack variable, and so is generally discarded after
is a slack variable, and so is generally discarded after 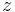 is found. As such, the problem can also be formulated as:
is found. As such, the problem can also be formulated as:
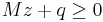
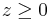
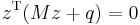 (the complementarity condition)
(the complementarity condition)
Convex quadratic-minimization: Minimum conditions
Finding a solution to the linear complementarity problem is associated with minimizing the quadratic function
subject to the constraints
These constraints ensure that f is always non-negative. The minimum of f is 0 at z if and only if z solves the linear complementarity problem.
If M is positive definite, any algorithm for solving (strictly) convex QPs can solve the LCP. Specially designed basis-exchange pivoting algorithms, such as Lemke's algorithm and a variant of the simplex algorithm of Dantzig have been used for decades. Besides having polynomial time complexity, interior-point methods are also effective in practice.
Also, a quadratic-programming problem stated as minimize 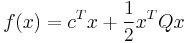 subject to
subject to 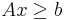 as well as
as well as 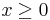 with Q symmetric
with Q symmetric
is the same as solving the LCP with
This is because the Karush–Kuhn–Tucker conditions of the QP problem can be written as:
...being 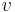 the Lagrange multipliers on the non-negativity constraints,
the Lagrange multipliers on the non-negativity constraints,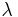 the multipliers on the inequality constraints, and
the multipliers on the inequality constraints, and 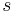 the slack variables for the inequality constraints. The fourth condition derives from the complementarity of each group of variables (
the slack variables for the inequality constraints. The fourth condition derives from the complementarity of each group of variables (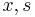 ) with its set of KKT vectors (optimal Lagrange multipliers) being (
) with its set of KKT vectors (optimal Lagrange multipliers) being (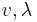 ).
).
In that case,
If the non-negativity constraint on the 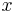 is relaxed, the dimensionality of the LCP problem can be reduced to the number of the inequalities, as long as
is relaxed, the dimensionality of the LCP problem can be reduced to the number of the inequalities, as long as 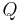 is non-singular (which is guaranteed if it is positive definite). The multipliers
is non-singular (which is guaranteed if it is positive definite). The multipliers 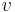 are no longer present, and the first KKT conditions can be rewritten as:
are no longer present, and the first KKT conditions can be rewritten as:
or:
pre-multiplying the two sides by 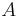 and subtracting
and subtracting 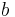 we obtain:
we obtain:
The left side, due to the second KKT condition, is 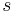 . Substituting and reordering:
. Substituting and reordering:
Calling now 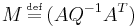 and
and 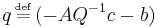 we have an LCP, due to the relation of complementarity between the slack variables
we have an LCP, due to the relation of complementarity between the slack variables 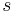 and their Lagrange multipliers
and their Lagrange multipliers 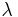 . Once we solve it, we may obtain the value of
. Once we solve it, we may obtain the value of 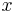 from
from 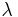 through the first KKT condition.
through the first KKT condition.
Finally, it is also possible to handle additional equality constraints:
This introduces a vector of Lagrange multipliers 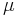 , with the same dimension as
, with the same dimension as 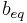 .
.
It is easy to verify that the 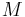 and
and 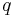 for the LCP system
for the LCP system 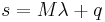 are now expressed as:
are now expressed as:
From 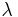 we can now recover the values of both
we can now recover the values of both 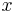 and the Lagrange multiplier of equalities
and the Lagrange multiplier of equalities 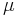 :
:
![\left[\begin{array}{c}{x}\\ {\mu}\end{array}\right] = \left[\begin{array}{cc} {Q} & {A}_{eq}^{T}\\ -{A}_{eq} & {0}\end{array}\right]^{-1} \left[\begin{array}{c} {A}^{T}{\lambda}-{c}\\-{b}_{eq}\end{array}\right] \,](/2012-wikipedia_en_all_nopic_01_2012/I/31c980b50228d0ebf734c24f95208d03.png)
In fact, most QP solvers work on the LCP formulation, including the interior point method, principal / complementarity pivoting, and active set methods.[1][2] LCP problems can be solved also by the criss-cross algorithm,[4][5][6][7] conversely, for linear complementarity problems, the criss-cross algorithm terminates finitely only if the matrix is a sufficient matrix.[6][7] A sufficient matrix is a generalization both of a positive-definite matrix and of a P-matrix, whose principal minors are each positive.[8][6][7] Such LCPs can be solved when they are formulated abstractly using oriented-matroid theory.[9][10][11]
See also
- Complementarity theory
- Physics engine Impulse/constraint type physics engines for games use this approach.
Notes
- ^ a b Murty (1988)
- ^ a b Cottle, Pang & Stone (1992)
- ^ R. W. Cottle and G. B. Dantzig. Complementary pivot theory of mathematical programming. Linear Algebra and its Applications, 1:103-125, 1968.
- ^ Fukuda & Namiki (1994)
- ^ Fukuda & Terlaky (1997)
- ^ a b c den Hertog, D.; Roos, C.; Terlaky, T. (1 July 1993). "The linear complementarity problem, sufficient matrices, and the criss-cross method" (pdf). Linear Algebra and its Applications 187: 1–14. doi:10.1016/0024-3795(93)90124-7. http://arno.uvt.nl/show.cgi?fid=72943.
- ^ a b c Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software 21 (2): 247–266. doi:10.1080/10556780500095009. MR2195759. http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf.
- ^ Cottle, R. W.; Pang, J.-S.; Venkateswaran, V. (March–April 1989). "Sufficient matrices and the linear complementarity problem". Linear Algebra and its Applications 114–115: 231–249. doi:10.1016/0024-3795(89)90463-1. MR986877. http://www.sciencedirect.com/science/article/pii/0024379589904631.
- ^ Todd (1985)
- ^ Terlaky & Zhang (1993): Terlaky, Tamás; Zhang, Shu Zhong (1993). "Pivot rules for linear programming: A Survey on recent theoretical developments". Annals of Operations Research (Springer Netherlands) 46–47 (1): 203–233. doi:10.1007/BF02096264. ISSN 0254-5330. MR1260019. PDF file of (1991) preprint.
- ^ Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999). "10 Linear programming". Oriented Matroids. Cambridge University Press. pp. 417–479. doi:10.1017/CBO9780511586507. ISBN 9780521777506. MR1744046. http://ebooks.cambridge.org/ebook.jsf?bid=CBO9780511586507.
References
- Cottle, Richard W.; Pang, Jong-Shi; Stone, Richard E. (1992). The linear complementarity problem. Computer Science and Scientific Computing. Boston, MA: Academic Press, Inc.. pp. xxiv+762 pp.. ISBN 0-12-192350-9. MR1150683.
- Cottle, R. W.; Pang, J.-S.; Venkateswaran, V. (March–April 1989). "Sufficient matrices and the linear complementarity problem". Linear Algebra and its Applications 114–115: 231–249. doi:10.1016/0024-3795(89)90463-1. MR986877. http://www.sciencedirect.com/science/article/pii/0024379589904631.
- Csizmadia, Zsolt; Illés, Tibor (2006). "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf). Optimization Methods and Software 21 (2): 247–266. doi:10.1080/10556780500095009. MR2195759. http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf.
- Fukuda, Komei; Namiki, Makoto (March 1994). "On extremal behaviors of Murty's least index method". Mathematical Programming 64 (1): 365–370. doi:10.1007/BF01582581. MR1286455.
- den Hertog, D.; Roos, C.; Terlaky, T. (1 July 1993). "The linear complementarity problem, sufficient matrices, and the criss-cross method" (pdf). Linear Algebra and its Applications 187: 1–14. doi:10.1016/0024-3795(93)90124-7. http://arno.uvt.nl/show.cgi?fid=72943.
- Murty, K. G. (1988). Linear complementarity, linear and nonlinear programming. Sigma Series in Applied Mathematics. 3. Berlin: Heldermann Verlag. pp. xlviii+629 pp.. ISBN 3-88538-403-5. MR949214. Updated and free PDF version at Katta G. Murty's website. http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/.
- Fukuda, Komei; Terlaky, Tamás (1997). Thomas M. Liebling and Dominique de Werra. ed. "Criss-cross methods: A fresh view on pivot algorithms". Mathematical Programming: Series B (Amsterdam: North-Holland Publishing Co.) 79 (Papers from the 16th International Symposium on Mathematical Programming held in Lausanne, 1997): 369–395. doi:10.1016/S0025-5610(97)00062-2. MR1464775. Postscript preprint.
- Todd, Michael J. (1985). "Linear and quadratic programming in oriented matroids". Journal of Combinatorial Theory. Series B 39 (2): 105–133. doi:10.1016/0095-8956(85)90042-5. MR811116.
Further reading
- R. W. Cottle and G. B. Dantzig. Complementary pivot theory of mathematical programming. Linear Algebra and its Applications, 1:103-125, 1968.
- Terlaky, Tamás; Zhang, Shu Zhong (1993). "Pivot rules for linear programming: A Survey on recent theoretical developments". Annals of Operations Research (Springer Netherlands) 46–47 (1): 203–233. doi:10.1007/BF02096264. ISSN 0254-5330. MR1260019. PDF file of (1991) preprint.
External links
- LCPSolve — A simple procedure in GAUSS to solve a linear complementarity problem
- LCPSolve.py — A Python/NumPy implementation of LCPSolve is part of OpenOpt since its release 0.32
|
||||||||
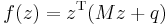
![{q} = \left[\begin{array}{c}{c}\\-{b}\end{array}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/b7cd9cc65783c92f8cb6c9258d717bb1.png)
![{M} = \left[\begin{array}{cc} {Q} & -{A}^{T}\\ {A} & 0\end{array}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/9a607f3766998b052043a8e2992be044.png)
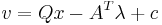
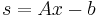
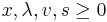
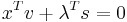
![{z} = \left[\begin{array}{c}{x}\\ {\lambda}\end{array}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/79a0760c24da1f75fddc2878be93f174.png)
![{w} = \left[\begin{array}{c}{v}\\ {s}\end{array}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/ff0cdf30056a55d6a966e817ac21ef86.png)
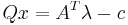
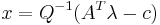
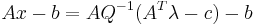
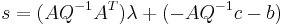
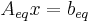
![{M} ~\overset{\underset{\mathrm{def}}{}}{=}~ (\left[\begin{array}{cc}{A} & {0}\end{array}\right] \left[\begin{array}{cc} {Q} & {A}_{eq}^{T}\\ -{A}_{eq} & {0}\end{array}\right]^{-1} \left[\begin{array}{cc}{A}^{T} \\ {0}\end{array}\right])\,](/2012-wikipedia_en_all_nopic_01_2012/I/c7ac3048d6005284ea82bf0849be6989.png)
![{q} ~\overset{\underset{\mathrm{def}}{}}{=}~ (- \left[\begin{array}{cc}{A} & {0}\end{array}\right] \left[\begin{array}{cc} {Q} & {A}_{eq}^{T}\\ -{A}_{eq} & {0}\end{array}\right]^{-1} \left[\begin{array}{c}{c}\\ {b}_{eq}\end{array}\right] - {b})\,](/2012-wikipedia_en_all_nopic_01_2012/I/aca43110fb47141040578dabb7b64130.png)